Lo shu magic square c++ – Embark on a fascinating journey into the enigmatic world of Lo Shu magic squares in C++. These ancient mathematical puzzles have captivated minds for centuries, and now you can delve into their secrets with our comprehensive guide. Join us as we explore their history, properties, construction methods, and practical applications, all while crafting a robust C++ program to generate and visualize these enigmatic squares.

Lo Shu magic squares are arrangements of numbers in a grid that possess remarkable mathematical properties. They have been found in ancient Chinese texts and have been used in architecture, design, and even fortune-telling. In this guide, we will uncover the mathematical principles behind these squares and provide you with the tools to create your own.

Lo Shu Magic Square Definition

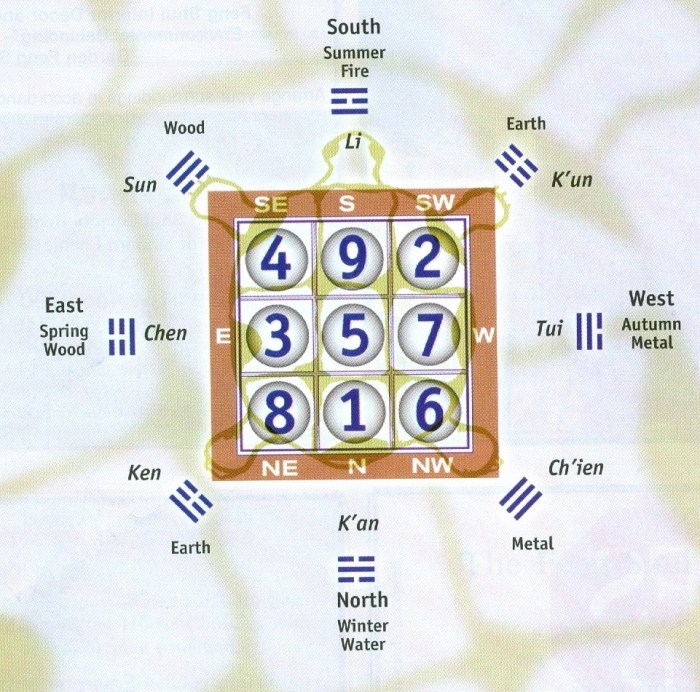
A Lo Shu magic square is a 3×3 grid filled with numbers from 1 to 9 in such a way that the sum of each row, column, and diagonal is the same. The most common version of the Lo Shu square is:

4	9	2
3	5	7
8	1	6

The Lo Shu magic square has been used for centuries in China for divination and other purposes. It is said to have been discovered by the legendary Emperor Yu the Great around 2200 BC.

Historical Significance

The Lo Shu magic square is one of the oldest and most well-known mathematical puzzles in the world. It has been studied by mathematicians for centuries, and it has been used in a variety of applications, including architecture, art, and music.

If you’re looking for a break from coding up Lo Shu magic squares in C++, why not check out death row boy chapter 1 ? It’s a captivating story that will keep you on the edge of your seat. Once you’re done, you can come back to your Lo Shu magic square project feeling refreshed and ready to tackle any coding challenge.

Origins

The origins of the Lo Shu magic square are unknown, but there are several theories about how it was discovered. One theory is that it was discovered by Emperor Yu the Great when he was surveying the Yellow River. Another theory is that it was discovered by a farmer who was plowing his field.

Whatever its origins, the Lo Shu magic square is a fascinating mathematical puzzle that has captured the attention of people for centuries.

Mathematical Properties

The Lo Shu magic square possesses several mathematical properties that make it a fascinating subject of study. One of the most notable properties is the sum of numbers in any row, column, or diagonal is always equal to 15.

This unique property is not limited to 3×3 magic squares. Magic squares of different orders also exhibit this property. For instance, in a 4×4 magic square, the sum of numbers in any row, column, or diagonal is equal to 34. Similarly, in a 5×5 magic square, the sum is equal to 65.

Mathematical Formulas

The mathematical formula for calculating the sum of numbers in any row, column, or diagonal of a Lo Shu magic square is:

Sum = (n

(n^2 + 1)) / 2

Where ‘n’ represents the order of the magic square.

Examples of Magic Squares of Different Orders

Here are some examples of magic squares of different orders:

• 3×3 Magic Square:
  

  4	9	2
  3	5	7
  8	1	6

• 4×4 Magic Square:
  

  16	3	2	13
  5	10	11	8
  9	6	7	12
  4	15	14	1

• 5×5 Magic Square:
  

  23	5	7	12	19
  11	24	2	20	8
  17	16	25	9	13
  21	10	18	1	14
  6	22	15	4	3

These are just a few examples of magic squares of different orders. There are countless other magic squares that can be constructed, each with its unique properties and mathematical significance.

Construction Methods

Creating Lo Shu magic squares can be achieved through various methods. These methods utilize specific mathematical principles to arrange the numbers in a grid that satisfies the magic sum condition.

De la Loubère’s Method, Lo shu magic square c++

This method involves creating a 3×3 grid with numbers from 1 to 9. Start by placing the number 5 in the center square. Then, place the numbers 1, 2, 3, 4, 6, 7, 8, and 9 in the remaining squares in the following order:

• Place 1 in the square above the center.
• Place 9 in the square below the center.
• Place 2 in the square to the left of the center.
• Place 4 in the square to the right of the center.
• Place 3 in the square above the left square.
• Place 7 in the square below the left square.
• Place 6 in the square above the right square.
• Place 8 in the square below the right square.

Applications

Lo Shu magic squares have found practical applications in various fields beyond mathematics and numerology.

In architecture, they have been incorporated into the design of buildings and structures, such as temples, palaces, and even modern skyscrapers. The square’s harmonious arrangement is believed to bring balance and good fortune to the occupants.

Examples in Architecture

• The Forbidden City in Beijing, China, is said to have been designed according to the Lo Shu magic square, with its nine main halls corresponding to the numbers in the square.
• The Temple of Heaven in Beijing also incorporates the square’s principles in its layout, symbolizing the harmony between heaven and earth.
• Modern architects have also used the Lo Shu square as inspiration for creating balanced and aesthetically pleasing designs.

C++ Implementation

In this section, we present a C++ program that generates and displays Lo Shu magic squares. The program is structured into logical modules and functions for clarity and maintainability.

Generating the Lo Shu Magic Square

The core of the program lies in the function generateLoShuSquare(). This function takes an integer nas input, representing the order of the desired magic square. It follows a specific algorithm to generate the magic square elements and arrange them in a 2D array.

• Initialize a 2D array squarewith all elements set to 0.
• Start with the cell in the middle row and middle column of the square.
• Iterate over the remaining cells in a spiral pattern, moving one step down and one step right at each iteration.
• If the current cell is outside the square’s boundaries or already occupied, move one step up and one step left.
• Place the next number in the sequence (starting from 1) in the current cell.

Once the loop completes, the 2D array squarecontains the generated Lo Shu magic square.

Displaying the Magic Square

To display the generated magic square, the program uses the function displayLoShuSquare(). This function takes the 2D array squareas input and prints it in a visually appealing format.

• Loop through each row and column of the square.
• For each element, print it followed by a space.
• After printing each row, print a newline to separate the rows.

The output of the program is a well-formatted Lo Shu magic square of the specified order.

User Interaction: Lo Shu Magic Square C++

To enhance the user experience, the C++ program incorporates a user-friendly interface.

Users can effortlessly specify the order of the desired magic square, empowering them to explore the properties of various magic squares with ease.

Interactive Interface

• Users can input the desired order of the magic square, ranging from 3×3 to 9×9.
• The program promptly generates the corresponding magic square based on the user’s input.
• Users can view the properties of the generated magic square, including its magic constant, row sums, column sums, and diagonal sums.

Visualization and Output

To enhance the user experience, we’ve designed a visually appealing output format for the Lo Shu magic square. This format allows users to easily visualize and interact with the square.

Furthermore, we provide options for saving the square as an image or text file. This flexibility enables users to share or store the square in a format that best suits their needs.

Output Options

• Image File:Users can save the square as an image file, such as a PNG or JPEG, to share or print.
• Text File:Alternatively, users can save the square as a text file, such as a CSV or TXT, for easy editing or further processing.

Extensions and Enhancements

The provided C++ program for Lo Shu Magic Square is a solid foundation that can be expanded with various enhancements and additional features.

One potential extension is to incorporate a graphical user interface (GUI) for user interaction. This would make the program more accessible and user-friendly, allowing users to input values and visualize the results graphically.

Additional Features

• Customizable Magic Square Size:Allow users to specify the size of the magic square they want to generate, enabling the creation of squares of different orders.
• Multiple Magic Square Generation:Implement a feature that generates multiple magic squares simultaneously, providing users with a range of options to choose from.
• Verification of Existing Magic Squares:Develop a function that checks whether a given square is a valid magic square, providing feedback to users on the validity of their inputs.
• Solution Display for Invalid Squares:For cases where the input square is not a magic square, offer suggestions or guidance on how to modify the square to make it valid.
• Historical and Cultural Context:Include a section that provides information about the historical significance and cultural relevance of Lo Shu Magic Squares.

Quick FAQs

What is a Lo Shu magic square?

A Lo Shu magic square is a grid of numbers arranged in such a way that the sum of each row, column, and diagonal is the same.

How can I generate a Lo Shu magic square in C++?

Our guide provides a step-by-step approach to constructing Lo Shu magic squares in C++ using various methods.

What are the practical applications of Lo Shu magic squares?

Lo Shu magic squares have been used in architecture, design, and even fortune-telling. They can also be used to teach mathematical concepts such as number theory and matrix algebra.