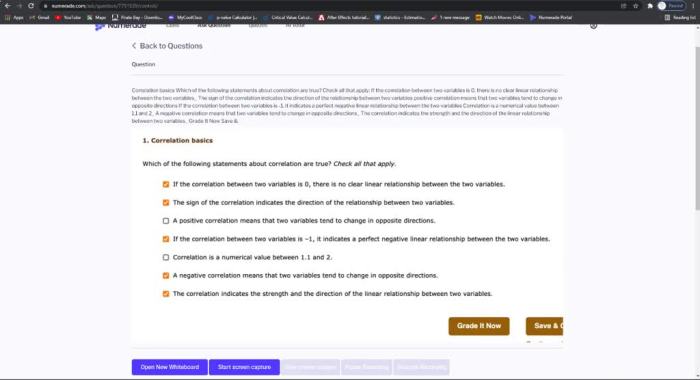
Which of the following statements about correlation is true? This question delves into the intriguing realm of statistics, where we explore the intricate relationship between variables and their potential interdependence. Correlation, a fundamental concept in this field, unveils the extent to which two variables tend to vary together, providing valuable insights into the nature of their association.
To fully grasp the significance of correlation, we must first comprehend its fundamental principles. Correlation measures the strength and direction of the linear relationship between two variables, ranging from perfect positive correlation, indicating a direct proportional relationship, to perfect negative correlation, suggesting an inverse proportional relationship.
Understanding the nuances of correlation empowers us to make informed decisions and draw meaningful conclusions from data.
Correlation Overview: Which Of The Following Statements About Correlation Is True
Correlation is a statistical measure that describes the relationship between two or more variables. It indicates the extent to which two variables vary together, either in the same direction or in opposite directions.
There are different types of correlations:
- Positive correlation:As one variable increases, the other variable also increases.
- Negative correlation:As one variable increases, the other variable decreases.
- Zero correlation:There is no relationship between the two variables.
Correlation and Causation
It is important to note that correlation does not imply causation. Just because two variables are correlated does not mean that one variable causes the other.
For example, there is a strong positive correlation between ice cream sales and drowning deaths. However, this does not mean that eating ice cream causes drowning. Instead, both ice cream sales and drowning deaths are likely influenced by a third factor, such as warm weather.
Measuring Correlation
The Pearson correlation coefficient is a common measure of correlation. It ranges from -1 to 1, where:
- -1:Perfect negative correlation
- 0:No correlation
- 1:Perfect positive correlation
A positive value indicates a positive correlation, while a negative value indicates a negative correlation.
Other measures of correlation include:
- Spearman’s rank correlation coefficient
- Kendall’s tau correlation coefficient
Using Correlation in Data Analysis, Which of the following statements about correlation is true
Correlation is a useful tool for identifying trends and patterns in data. It can be used in a variety of fields, including:
- Economics:To study the relationship between economic variables, such as inflation and unemployment.
- Medicine:To investigate the relationship between risk factors and diseases.
- Marketing:To understand the relationship between advertising and sales.
However, it is important to remember that correlation does not imply causation. When interpreting correlations, it is important to consider other factors that may be influencing the relationship.
FAQ Compilation
What is the difference between correlation and causation?
Correlation measures the strength and direction of the linear relationship between two variables, while causation implies that one variable directly influences the other.
How do you interpret the value of the Pearson correlation coefficient?
The Pearson correlation coefficient ranges from -1 to 1. A value close to 1 indicates a strong positive correlation, while a value close to -1 indicates a strong negative correlation. A value close to 0 indicates no correlation.
What are some limitations of using correlation in data analysis?
Correlation does not imply causation. It is possible for two variables to be correlated even if they are not causally related. Additionally, correlation can be affected by outliers and non-linear relationships.