How to write absolute value functions as piecewise functions – Embark on a journey into the realm of piecewise functions, where we unravel the intricate art of expressing absolute value functions in a piecewise manner. This comprehensive guide delves into the fundamental concepts, step-by-step construction methods, and practical applications of these versatile mathematical tools.
By exploring the interplay between absolute value functions and piecewise functions, we gain a deeper understanding of their unique properties and their ability to model real-world scenarios. Join us as we unveil the secrets of piecewise function construction and discover the power of these functions in solving complex mathematical problems.
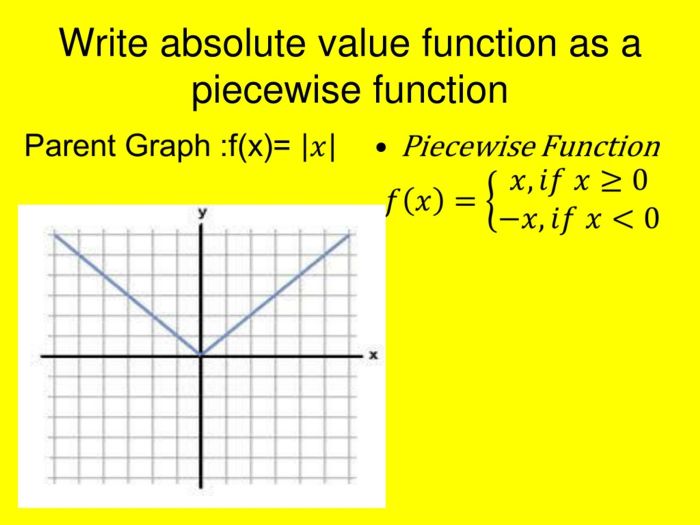
Definition of Absolute Value Functions
Absolute value functions are mathematical functions that map real numbers to their non-negative counterparts. They are defined as follows:
|x| = x, if x ≥ 0|x| =-x, if x< 0
Piecewise Functions
Piecewise functions are functions that are defined differently for different intervals of their domain. They can be used to represent absolute value functions as follows:
- f(x) = x, if x ≥ 0
- f(x) = -x, if x< 0
Creating Piecewise Functions for Absolute Value Functions, How to write absolute value functions as piecewise functions
To create a piecewise function for an absolute value function, follow these steps:
- Identify the intervals where the function is positive and negative.
- Define the function as x for the positive interval and
x for the negative interval.
- Combine the two functions into a single piecewise function.
Example:
Create a piecewise function for the absolute value function |x|.
- Positive interval: x ≥ 0
- Negative interval: x< 0
- Piecewise function: f(x) = x, if x ≥ 0; -x, if x< 0
Examples of Piecewise Functions for Absolute Value Functions
| Absolute Value Function | Piecewise Function | Graphical Representation |
|---|---|---|
| |x| | f(x) = x, if x ≥ 0;
|
 |
|x
|
f(x) = x
|
 |
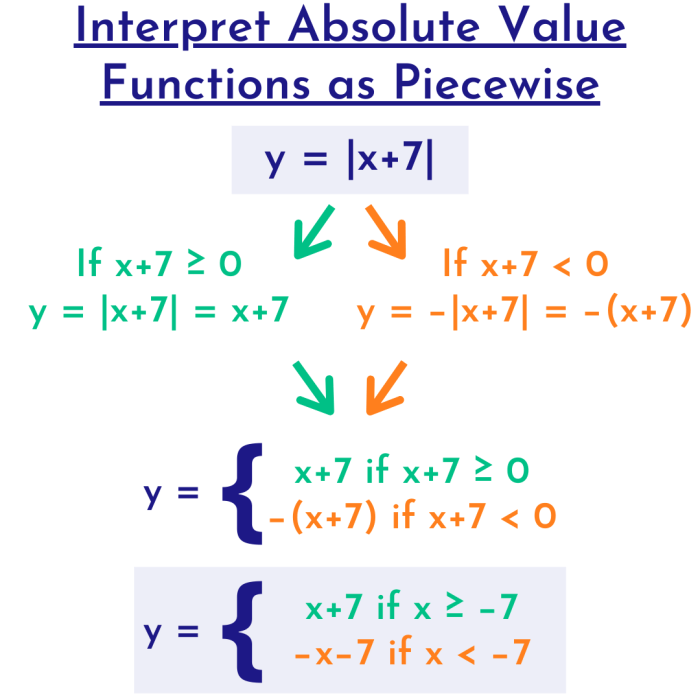
| |x + 2| | f(x) = x + 2, if x ≥
-(x + 2), if x < -2 |
 |
Applications of Piecewise Functions for Absolute Value Functions
Piecewise functions for absolute value functions have various real-world applications, including:
- Calculating distances: The absolute value of a number represents its distance from zero on the number line. This property can be used to calculate distances between points on a coordinate plane.
- Modeling rectifiers: Rectifiers are electronic devices that convert alternating current (AC) to direct current (DC). The piecewise function for an absolute value function can be used to model the output of a rectifier.
- Measuring errors: The absolute value of the difference between two values represents the error in a measurement. This property can be used to calculate the accuracy of measurements.
Additional Considerations
When creating piecewise functions for absolute value functions, consider the following:
- The piecewise function must be continuous at the boundary between the positive and negative intervals.
- The piecewise function must be differentiable at the boundary between the positive and negative intervals, if necessary.
- The piecewise function may have special cases, such as when the boundary between the positive and negative intervals is not a whole number.
Answers to Common Questions: How To Write Absolute Value Functions As Piecewise Functions
What are the key advantages of using piecewise functions to represent absolute value functions?
Piecewise functions offer several advantages: they simplify complex absolute value functions, enable easier analysis of different intervals, and provide a flexible framework for modeling real-world scenarios where absolute values arise.
How can I determine the piecewise function for a given absolute value function?
To construct the piecewise function, identify the different intervals where the absolute value function takes on positive and negative values. Define the corresponding linear functions for each interval, ensuring that they intersect at the origin.
What are some common applications of piecewise functions for absolute value functions?
Piecewise functions for absolute value functions find applications in various fields, including physics (modeling motion with friction), economics (representing piecewise linear cost functions), and computer science (implementing absolute value calculations efficiently).